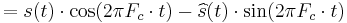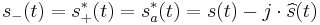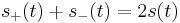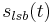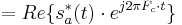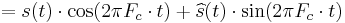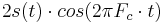Single-sideband modulation
| Passband modulation |
|---|
| Analog modulation |
| AM · SSB · QAM · FM · PM · SM |
| Digital modulation |
| FSK · MFSK · ASK · OOK · PSK · QAM MSK · CPM · PPM · TCM · SC-FDE |
| Spread spectrum |
| CSS · DSSS · FHSS · THSS |
| See also: Demodulation, modem, line coding, PAM, PWM, PCM |
Single-sideband modulation (SSB) or Single-sideband suppressed-carrier (SSB-SC) is a refinement of amplitude modulation that more efficiently uses electrical power and bandwidth.
Amplitude modulation produces a modulated output signal that has twice the bandwidth of the original baseband signal. Single-sideband modulation avoids this bandwidth doubling, and the power wasted on a carrier, at the cost of somewhat increased device complexity.
Contents |
History
The first U.S. patent[1] for SSB modulation was applied for on December 1, 1915 by John Renshaw Carson. The U.S. Navy experimented with SSB over its radio circuits before World War I.[2][3] SSB first entered commercial service on January 7, 1927 on the longwave transatlantic public radiotelephone circuit between New York and London. The high power SSB transmitters were located at Rocky Point, New York and Rugby, England. The receivers were in very quiet locations in Houlton, Maine and Cupar Scotland.[4]
SSB was also used over long distance telephone lines, as part of a technique known as frequency-division multiplexing (FDM). FDM was pioneered by telephone companies in the 1930s. This enabled many voice channels to be sent down a single physical circuit, for example in L-carrier. SSB allowed channels to be spaced (usually) just 4,000 Hz apart, while offering a speech bandwidth of nominally 300–3,400 Hz.
Amateur radio operators began serious experimentation with SSB after World War II. The Strategic Air Command established SSB as the radio standard for its aircraft in 1957.[5] It has become a de facto standard for long-distance voice radio transmissions since then.
Mathematical formulation
SSB and vestigial side band (VSB) can also be regarded mathematically as special cases of analog quadrature amplitude modulation.
Let 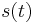 be the baseband waveform to be transmitted. Its Fourier transform,
be the baseband waveform to be transmitted. Its Fourier transform, 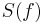 , is Hermitian symmetrical about the
, is Hermitian symmetrical about the  axis, because
axis, because 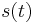 is real-valued. Double sideband modulation of
is real-valued. Double sideband modulation of  to a radio transmission frequency,
to a radio transmission frequency, 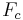 , moves the axis of symmetry to
, moves the axis of symmetry to 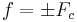 , and the two sides of each axis are called sidebands.
, and the two sides of each axis are called sidebands.
Let 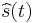 represent the Hilbert transform of
represent the Hilbert transform of 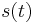 . Then
. Then
is a useful mathematical concept, called an analytic signal. The Fourier transform of 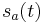 equals
equals 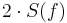 , for
, for 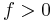 , but it has no negative-frequency components. So it can be modulated to a radio frequency and produce just a single sideband.
, but it has no negative-frequency components. So it can be modulated to a radio frequency and produce just a single sideband.
The analytic representation of 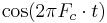 is:
is:
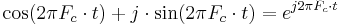 (the equality is Euler's formula)
(the equality is Euler's formula)
whose Fourier transform is 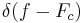 .
.
When 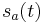 is modulated (i.e. multiplied) by
is modulated (i.e. multiplied) by 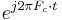 , all frequency components are shifted by
, all frequency components are shifted by 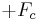 , so there are still no negative-frequency components. Therefore, the complex product is an analytic representation of the single sideband signal:
, so there are still no negative-frequency components. Therefore, the complex product is an analytic representation of the single sideband signal:
where 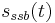 is the real-valued, single sideband waveform. Therefore:
is the real-valued, single sideband waveform. Therefore:
The presence of two out-of-phase (quadrature) carrier waves is now evident.
Lower sideband
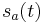 represents the baseband signal's upper sideband,
represents the baseband signal's upper sideband, 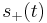 . It is also possible, and useful, to convey the baseband information using its lower sideband,
. It is also possible, and useful, to convey the baseband information using its lower sideband, 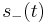 , which is a mirror image about f=0 Hz. By a general property of the Fourier transform, that symmetry means it is the complex conjugate of
, which is a mirror image about f=0 Hz. By a general property of the Fourier transform, that symmetry means it is the complex conjugate of 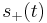 :
:
Note that:
The gain of 2 is a result of defining the analytic signal (one sideband) to have the same total energy as 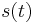 (both sidebands).
(both sidebands).
As before, the signal is modulated by 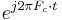 . The typical
. The typical 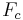 is large enough that the translated lower sideband (LSB) has no negative-frequency components. Then the result is another analytic signal, whose real part is the actual transmission.
is large enough that the translated lower sideband (LSB) has no negative-frequency components. Then the result is another analytic signal, whose real part is the actual transmission.
Note that the sum of the two sideband signals is
which is the classic model of suppressed-carrier double sideband AM.
Practical implementations
Bandpass filtering
A signal at frequency 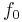 amplitude-modulated onto a carrier wave at
amplitude-modulated onto a carrier wave at 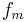 can be expressed as simple multiplication of two cosine waves:
can be expressed as simple multiplication of two cosine waves: 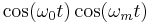 , where
, where 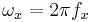 . Applying a simple trigonometric identity, we can change the above expression to be
. Applying a simple trigonometric identity, we can change the above expression to be 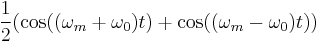 . Each cosine term in the equation is known as a sideband.
. Each cosine term in the equation is known as a sideband.
One method of producing an SSB signal is to remove one of the sidebands via filtering, leaving only either the upper sideband (USB), the sideband with the higher frequency, or less commonly the lower sideband (LSB), the sideband with the lower frequency. Most often, the carrier is reduced or removed entirely (suppressed), being referred to in full as single sideband suppressed carrier (SSBSC). Assuming both sidebands are symmetric, which is the case for a normal AM signal, no information is lost in the process. Since the final RF amplification is now concentrated in a single sideband, the effective power output is greater than in normal AM (the carrier and redundant sideband account for well over half of the power output of an AM transmitter). Though SSB uses substantially less bandwidth and power, it cannot be demodulated by a simple envelope detector like standard AM.
Hartley modulator
An alternate method of generation known as a Hartley modulator, named after R. V. L. Hartley, uses phasing to suppress the unwanted sideband. To generate an SSB signal with this method, two versions of the original signal are generated, mutually 90° out of phase for any single frequency within the operating bandwidth. Each one of these signals then modulates carrier waves (of one frequency) that are also 90° out of phase with each other. By either adding or subtracting the resulting signals, a lower or upper sideband signal results. A benefit of this approach is to allow an analytical expression for SSB signals, which can be used to understand effects such as synchronous detection of SSB.
Shifting the baseband signal 90° out of phase cannot be done simply by delaying it, as it contains a large range of frequencies. In analog circuits, a wideband 90-degree phase-difference network[6] is used. The method was popular in the days of vacuum-tube radios, but later gained a bad reputation due to poorly adjusted commercial implementations. Modulation using this method is again gaining popularity in the homebrew and DSP fields. This method, utilizing the Hilbert transform to phase shift the baseband audio, can be done at low cost with digital circuitry.
Weaver modulator
Another variation, the Weaver modulator,[7] uses only lowpass filters and quadrature mixers, and is a favored method in digital implementations.
In Weaver's method, the band of interest is first translated to be centered at zero, conceptually by modulating a complex exponential 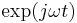 with frequency in the middle of the voiceband, but implemented by a quadrature pair of sine and cosine modulators at that frequency (e.g. 2 kHz). This complex signal or pair of real signals is then lowpass filtered to remove the undesired sideband that is not centered at zero. Then, the single-sideband complex signal centered at zero is upconverted to a real signal, by another pair of quadrature mixers, to the desired center frequency.
with frequency in the middle of the voiceband, but implemented by a quadrature pair of sine and cosine modulators at that frequency (e.g. 2 kHz). This complex signal or pair of real signals is then lowpass filtered to remove the undesired sideband that is not centered at zero. Then, the single-sideband complex signal centered at zero is upconverted to a real signal, by another pair of quadrature mixers, to the desired center frequency.
Demodulation
The front end of an SSB receiver is similar to that of an AM or FM receiver, consisting of a superheterodyne RF front end that produces a frequency-shifted version of the radio frequency (RF) signal within a standard intermediate frequency (IF) band.
To recover the original signal from the IF SSB signal, the single sideband must be frequency-shifted down to its original range of baseband frequencies, by using a product detector which mixes it with the output of a beat frequency oscillator (BFO). In other words, it is just another stage of heterodyning.(mixing down to base band). For this to work, the BFO frequency must be exactly adjusted. If the BFO frequency is off, the output signal will be frequency-shifted (up or down), making speech sound strange and "Donald Duck"-like, or unintelligible. For audio communications, there is a common agreement about the BFO oscillator shift of 1.7kHz. A voice signal is sensitive to about 50Hz shift, with up to 100Hz still bearable. Some receivers use a carrier recovery system, which attempts to automatically lock on to the exact IF frequency. The carrier recovery doesn't solve the frequency shift. It gives better S/N ratio on the detector output.
As an example, consider an IF SSB signal centered at frequency 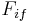 = 45000 Hz. The baseband frequency it needs to be shifted to is
= 45000 Hz. The baseband frequency it needs to be shifted to is 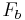 = 2000 Hz. The BFO output waveform is
= 2000 Hz. The BFO output waveform is 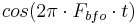 . When the signal is multiplied by (aka 'heterodyned with') the BFO waveform, it shifts the signal to
. When the signal is multiplied by (aka 'heterodyned with') the BFO waveform, it shifts the signal to 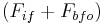 and to
and to 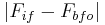 , which is known as the beat frequency or image frequency. The objective is to choose an
, which is known as the beat frequency or image frequency. The objective is to choose an 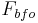 that results in
that results in 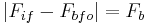 = 2000 Hz. (The unwanted components at
= 2000 Hz. (The unwanted components at 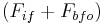 can be removed by a lowpass filter (for which an output transducer or the human ear may serve)).
can be removed by a lowpass filter (for which an output transducer or the human ear may serve)).
Note that there are two choices for 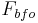 : 43000 Hz and 47000 Hz, a.k.a. low-side and high-side injection. With high-side injection, the spectral components that were distributed around 45000 Hz will be distributed around 2000 Hz in the reverse order, also known as an inverted spectrum. That is in fact desirable when the IF spectrum is also inverted, because the BFO inversion restores the proper relationships. One reason for that is when the IF spectrum is the output of an inverting stage in the receiver. Another reason is when the SSB signal is actually a lower sideband, instead of an upper sideband. But if both reasons are true, then the IF spectrum in not inverted, and the non-inverting BFO (43000 Hz) should be used.
: 43000 Hz and 47000 Hz, a.k.a. low-side and high-side injection. With high-side injection, the spectral components that were distributed around 45000 Hz will be distributed around 2000 Hz in the reverse order, also known as an inverted spectrum. That is in fact desirable when the IF spectrum is also inverted, because the BFO inversion restores the proper relationships. One reason for that is when the IF spectrum is the output of an inverting stage in the receiver. Another reason is when the SSB signal is actually a lower sideband, instead of an upper sideband. But if both reasons are true, then the IF spectrum in not inverted, and the non-inverting BFO (43000 Hz) should be used.
If 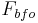 is off by a small amount, then the beat frequency is not exactly
is off by a small amount, then the beat frequency is not exactly 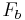 , which can lead to the speech distortion mentioned earlier.
, which can lead to the speech distortion mentioned earlier.
SSB as a speech-scrambling technique
SSB techniques can also be adapted to frequency-shift and frequency-invert baseband waveforms. These effects were used, in conjunction with other filtering techniques, during World War II as a simple method for speech encryption. Radiotelephone conversations between the US and Britain were intercepted and "decrypted" by the Germans; they included some early conversations between Franklin D. Roosevelt and Churchill. In fact, the signals could be understood directly by trained operators. Largely to allow secure communications between Roosevelt and Churchill, the SIGSALY system of digital encryption was devised.
Today, such simple inversion-based speech encryption techniques are easily decrypted using simple techniques and are no longer regarded as secure.
Vestigial sideband (VSB)
A vestigial sideband (in radio communication) is a sideband that has been only partly cut off or suppressed. Television broadcasts (in analog video formats) use this method if the video is transmitted in AM, due to the large bandwidth used. It may also be used in digital transmission, such as the ATSC standardized 8-VSB. The Milgo 4400/48 modem (circa 1967) used vestigial sideband and phase-shift keying to provide 4800-bit/s transmission over a 1600 Hz channel.
The video baseband signal used in TV in countries that use NTSC or ATSC has a bandwidth of 6 MHz. To conserve bandwidth, SSB would be desirable, but the video signal has significant low frequency content (average brightness) and has rectangular synchronising pulses. The engineering compromise is vestigial sideband modulation. In vestigial sideband the full upper sideband of bandwidth W2 = 4 MHz is transmitted, but only W1 = 1.25 MHz of the lower sideband is transmitted, along with a carrier. This effectively makes the system AM at low modulation frequencies and SSB at high modulation frequencies. The absence of the lower sideband components at high frequencies must be compensated for, and this is done by the RF and IF filters.
See also
- ACSSB, amplitude-companded single sideband
- Independent sideband
- Modulation for other examples of modulation techniques
- Sideband for more general information about a sideband
References
- ^ US 1449382 John Carson/AT&T: "Method and Means for Signaling with High Frequency Waves" filed on December 1, 1915; granted on March 27, 1923
- ^ The History of Single Sideband Modulation, Ing. Peter Weber
- ^ IEEE, Early History of Single-Sideband Transmission, Oswald, A.A.
- ^ History Of Undersea Cables, (1927)
- ^ "Amateur Radio and the Rise of SSB" (PDF). National Association for Amateur Radio. http://www.arrl.org/files/file/Technology/pdf/McElroy.pdf.
- ^ Earthlink.net, listing numerous articles.
- ^ "A Third Method of Generation and Detection of Single-Sideband Signals" D K Weaver Jr. Proc. IRE, Dec. 1956
General references
- Partly from Federal Standard 1037C in support of MIL-STD-188
Further reading
- Sgrignoli, G., W. Bretl, R. and Citta. (1995). "VSB modulation used for terrestrial and cable broadcasts." IEEE Transactions on Consumer Electronics. v. 41, issue 3, p. 367 - 382.
- J. Brittain, (1992). "Scanning the past: Ralph V.L. Hartley", Proc. IEEE, vol.80,p. 463.
|
||||||||||||||||||||||||||||||||
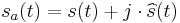
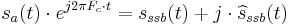
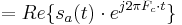
![= Re\left\{\ [s(t)%2Bj\cdot \widehat s(t)]\cdot [\cos(2\pi F_c\cdot t)%2Bj\cdot \sin(2\pi F_c\cdot t)]\ \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/253d65e0cbe061db1586c73320102ffa.png)